Calculabilitate si complexitate (Victor Mitrana)

De la Cursuri - Facultatea de Matematica si informatica

Salt la: navigare, căutare

5T4Bar <a href="http://sbsjhqcyhrlw.com/">sbsjhqcyhrlw</a>, [url=http://rfwjenbsyueu.com/]rfwjenbsyueu[/url], [link=http://qgqogljaixed.com/]qgqogljaixed[/link], http://szyltnfitmit.com/



Cuprins

2008-2009 - anul 2 - semestrul 1 - Domeniul de Informatica

Cursuri

  1. Calculabilitate:
    • Masina Turing
    • Functii Recursive
    • Programe Standard
  2. Complexitate
    • Clase de complexitate
      • timp
      • spatiu
      • NP
      • N
      • P Space
      • N Space

Descriere

  • 2 ore de curs / saptamana
  • 2 ora de seminar / saptamana
  • 5 credite

2, http://cheapmedsonline.co.uk/ cialis price,

Notare

  • examen: 2/3 din care:
    • teoretie 50%
    • probleme 50%
  • seminar 1/3
    • lucrare 70% din seminar
    • referat 20% din seminar

Bibliografie

  • M. Davis, E. Weynker - "Computability, Comprexity and Languages" - Academic Press, 1983
  • M. R. Garey, D. S. Johnson - "Computers and Intractability: A Guide to the Theory of NP Completeness" - W. H. Freeman, 1979
  • John E. Hopcroft, Jeffrey D. Ullman - "Introduction to Automata Theory, Languages and Computation" - Addison-Wesley 1979

Subiecte date la examen

  • cele 9 subiecte de pregatit pentru examen:

1. Functii calculabile si necalculabile cu programe standard

    • definim ce inseamna fct calculabila/necalculabila
    • proprietati
    • de demonstrat ca fct universala e calculabila si ca fct halt e necalculabila

2. Masini Turing

    • echivalenta MT cu gramatici(1 dem. pt examen)
    • echivalenta MTn cu MTd (1 dem)
    • enunturi pt toate

3. Echivalenta modelelor de calcul

    • functii Turing calculabile,recursive enumerabile,calculabile cu programe standard(definitii/enunturi)
    • relatia dintre ele
    • 3 incluziuni: (alegem fie Turing - recursiv, fie celelalte 2)
      • orice funtie Turing e recursiva
      • orice functie recursiva e calculabila
      • orice functie calculabila e Turing calculabila

4. Multimi recursive, recursiv enumerabile, nerecursiv enumerabile

    • enunturi
    • diferente intre ele
    • teorema lui Rice (o demonstratie - la punctul acesta sau la urmatorul)
    • exemplu de multime care e recursive si nu e recursiv enumerabila

5. Clasa de complexitate timp

    • definitia modelului
    • clasele
    • relatia cu clasa spatiu
    • reducerea constante si benzi (2 demonstratii la alegere)

6. Clasa de complexitate spatiu

    • la fel ca la timp

7. Ierarhii de clase de complexitate (separate sau impreuna, nu mi-e clar… ideea este ca daca le da separate, ele au o buna bucata comuna)

    • timp si spatiu
    • ce factor trebuie adaugat la o clasa de complexitate pentru a fi siguri ca obtinem o clasa de complexitate de ordin strict mai mare?
    • teoremele care separau clasele
    • teorema Savitch
    • lema de translatare
    • 2 demonstratii din 4, la alegere

8. Completitudine, reducere (sau NP-completitudine)

    • definitii/enunturi
    • la reducere, teorema data+demonstratie
    • 1 exemplu de problema NP-completa si sa aratam k e NP-completa

9. Reduceri. Probleme complete.

    • definitii
    • de ales o reducere si o completitudine
    • de ales o problema si sa aratam ca e completa



2007-2008 - anul 2 - semestrul 1 - Domeniul de Informatica

Cursuri

  1. Calculabilitate:
    • Masina Turing
    • Functii Recursive
    • Programe Standard
  2. Complexitate
    • Clase de complexitate
      • timp
      • spatiu
      • NP
      • N
      • P Space
      • N Space

Descriere

2, http://cheapmedsonline.co.uk/ cialis price,

Notare

  • de regula este:
    • examen: 2/3 din care:
      • teoretie 50%
      • probleme 50%
    • seminar 1/3
      • lucrare 2/3 din seminar - avem voie cu materiale
      • referat 1/3 din seminar - se poate recupera rezolvand in timpul examenului o problema in plus
  • nu se face prezenta

Bibliografie

  • M. Davis, E. Weynker - "Computability, Comprexity and Languages" - Academic Press, 1983
  • M. R. Garey, D. S. Johnson - "Computers and Intractability: A Guide to the Theory of NP Completeness" - W. H. Freeman, 1979
  • John E. Hopcroft, Jeffrey D. Ullman - "Introduction to Automata Theory, Languages and Computation" - Addison-Wesley 1979

Subiecte date la examen

  • cele 8 subiecte de pregatit pentru examen:
  1. Masini Turing
    • echivalenta MT cu gramatici(1 dem. pt examen)
    • echivalenta MTn cu MTd (1 dem)
    • enunturi pt toate
  2. Echivalenta modelelor de calcul
    • functii Turing calculabile,recursive enumerabile,calculabile cu programe standard(definitii/enunturi)
    • relatia dintre ele
    • 3 incluziuni: (alegem fie Turing - recursiv, fie celelalte 2)
      • orice funtie Turing e recursiva
      • orice functie recursiva e calculabila
      • orice functie calculabila e Turing calculabila
  3. Multimi recursive, recursiv enumerabile, nerecursiv enumerabile
    • enunturi
    • diferente intre ele
    • teorema lui Rice (o demonstratie - la punctul acesta sau la urmatorul)
    • exemplu de multime care e recursive si nu e recursiv enumerabila
  4. Clasa de complexitate timp
    • definitia modelului
    • clasele
    • relatia cu clasa spatiu
    • reducerea constante si benzi (2 demonstratii la alegere)
  5. Clasa de complexitate spatiu
    • la fel ca la timp
  6. Ierarhii de clase de complexitate
    • timp si spatiu
    • teoremele care separau clasele
    • teorema Savitch
    • lema de translatare
    • 2 demonstratii din 4, la alegere
  7. Completitudine, reducere
    • definitii/enunturi
    • la reducere, teorema data+demonstratie
    • 1 exemplu de problema NP-completa si sa aratam k e NP-completa
  • Grupa 232

1. Echivalenta modelelor de calcul 2. L = {w={1..9}{0..9}*, w reprezentare in baza 10 a unui nr, parte intreaga sup(sqrt(nr))= putere a lui 2} 3. problema in loc de referat: Problema ... este P completa. Demonstratie. P completa, nu NP completa!

lucrare: o masina Turing, de demonstrat ca 3 functii sunt primitiv recursive, una simpla, una cu functii pereche.

  • Grupa 233:

1. L={a^(n+[sqrt(n)])



2006-2007 - anul 2 - semestrul 1 - Domeniul de Informatica

Cursuri

  1. Calculabilitate:
    • Masina Turing
    • Functii Recursive
    • Programe Standard
  2. Complexitate
    • Clase de complexitate
      • timp
      • spatiu
      • NP
      • N
      • P Space
      • N Space

Descriere

2, http://cheapmedsonline.co.uk/ cialis price,

Notare

  • de regula este:
    • examen: 50% din care:
      • teoretie 50%
      • probleme 50%
      • este nevoie de minim 5 la teorie ca sa iti faca media cu nota de la probleme altfel se pica
    • seminar 50%
  • la noi a fost 2/3 exmenul si 1/3 seminarul ( s-a negogiat la ultimul curs )
  • nu se face prezenta

Bibliografie

  • M. Davis, E. Weynker - "Computability, Comprexity and Languages" - Academic Press, 1983
  • M. R. Garey, D. S. Johnson - "Computers and Intractability: A Guide to the Theory of NP Completeness" - W. H. Freeman, 1979
  • John E. Hopcroft, Jeffrey D. Ullman - "Introduction to Automata Theory, Languages and Computation" - Addison-Wesley 1979

Subiecte date la examen

  • cele 8 subiecte de pregatit pentru examen:
  1. Echivalenta masinilor Turing deterministe - nedeterministe
    • def mT; ce inseamna proces de calcul in mT;
    • toate rezultatele teoretice (adica 2) + 1 dem la alegere
  2. Echivalenta calculabile - functii recursive
    • def notiunilor
    • 3 incluziuni: (alegem fie Turing - recursiv, fie celelalte 2)
      • orice funtie Turing e recursiva
      • orice functie recursiva e calculabila
      • orice functie calculabila e Turing calculabila
  3. Multimi recursive, recursiv enumerabile, nerecursiv enumerabile
    • definitiile lor + proprietati
    • de dat exemple din fiecare si din exemplele astea, pt unul aratam k este asa (fara Rice si Post)
  4. Clasa de complexitate timp
    • definim modelul si clasele
    • reducerea constante si benzi
    • alegem benzi sau costante si le dem in detaliu
  5. Clasa de complexitate spatiu
    • la fel ca la timp
  6. Ierarhii de clase de complexitate (curs 10)
    • notiuni care apar - enunturi + 1 dem
  7. Legatura intre clasele de complexitate
    • enuntate notiunile si la alegere intre:
      • th Savitch sau
      • curs 10 - th care leaga: time - space, space - time (are 3 puncte)
  8. NP completitudine
    • cum se face reducerea
    • ce inseamna problema NP-completa
    • 1 exemplu de problema NP-completa si sa aratam k e NP-completa
  • la grupa 241
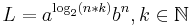
  1. L = {a^{\log_2(n*k)} b^n}, k \in \mathbb{N}
    • sa se construiasca o masina turing determinista care sa accepte acest limbaj
    • sa se estimeze numarul pe pasi pe care il face pe o intrare de lungime m
  2. dem ca f(n) = nk este spatiu construibila.
  • la grupa 243
  1. Echivalenta functii turing calc, calc si rec.
  2. dem ca functia f(n) = 3n e timp si spatiu construibila (cu cate o MT pt fiecare)
  • la grupa 244
  1. Functii recursive, calculabile, calculabile Turing.
  2. Sa se arate ca functia urmatoare este recursiva:
F(n) = F(n − 1)2 + F(n − 2)2
F(0) = 0,F(1) = 1
  • la grupa 242
  1. Functii recursive, calculabile, calculabile Turing.
  2. Sa se arate ca e functie recursiva:
F(0) = 4
F(1) = 4
F(n) = 2F(n − 1) + inf(log(F(n − 2)))
Adus de la "http://fmi.is-a-geek.net/index.php/Calculabilitate_si_complexitate_(Victor_Mitrana)"