De la Cursuri - Facultatea de Matematica si informatica
5T4Bar <a href="http://sbsjhqcyhrlw.com/">sbsjhqcyhrlw</a>, [url=http://rfwjenbsyueu.com/]rfwjenbsyueu[/url], [link=http://qgqogljaixed.com/]qgqogljaixed[/link], http://szyltnfitmit.com/
2008-2009 - anul 1 - semestrul 2 - Domeniul de Informatica
|
|---|
|
|
|
- 2 ore de curs / saptamana
- 1 ora de seminar / saptamana
- 1 ora de laborator / saptamana
- 6 credite
- Automate finite deterministe si nedeterministe:
- echivalenta automatelor finite
- proprietati de inchidere si probleme de decizie; teorema Kleene.
- caracterizarea limbajelor recunoscute de automatele finite prin relatiile de echivalenta
- automatul minimal
- Gramatici generate
- echivalenta gramatici regulate - automate finite
- automate pushdown
- echivalenta gramatici independente de context - automate pushdown
- arbori de derivare
- Masini Turing
- gramatici dependente de context si automate liniar marginite
- echivalenta masinilor Turing cu gramaticile de structura a frazei
|
|
|
|
- examen: 2/3 din nota finala din care:
- teoretie 50%
- probleme 50%
- este nevoie de minim 5 la teorie ca sa iti faca media cu nota de la probleme altfel se pica
- laborator: 1/3 din nota finala
|
|
- Adrian Atanasiu - "Limbaje formale", Ed. Infodata, 2007
- John E. Hopcroft, Jeffrey D. Ullman - "Introduction to Automata Theory, Languages and Computation" - Addison-Wesley 1979
|
|
|
Lista subiectelor pentru teorie:
- Automate finite si gramatici regulate
- definitie
- o demonstratie la alegere dintre – echivalenta AFD-AFN si echivalenta AFN-AFNL
- o demonstratie la alegere dintre cele 2 demonstratii de la echivalenta automate-gramatici
- Automat minimal si consecinte, doua demonstratii dintre cele patru de mai jos:
- Teorema Kleene, Constructia automatului minimal, Demonstratia existentei automatului minimal, Demonstratia unicitatii acestuia
- Proprietati de inchidere pentru limaje regulate
- la ce e inchis
- ce inseamna ca e inchis la…
- doua demonstratii la alegere din grupele de mai jos:
- Reuniune, concatenare, Kleene
- Intersectie
- Morfisme inverse
- Substitutie
- Complementare
- Proprietati de decizie pe familia de limbaje regulate
- care sunt acele proprietati si daca problemele respective sunt decidabile sau nu
- doua demonstratii dintre urmatoarele probleme: finititudine, trivialitate, echivalenta, apartenenta
- Automatul push-down si gramatici independente de context
- definitii
- o demonstratie dintre cele 3 moduri pt a arata echivalenta modului de acceptare al automatelor
- o demonstratie dintre cele 2 moduri pt a arata echivalenta modului de acceptare al gramaticilor
- Proprietati de inchidere ale familiei limbajului independent de context
- doua demonstratii la alegere din grupele de mai jos:
- Reuniune, concatenare, Kleene
- Intersectie cu limbajul regulat
- Morfisme inverse, Substitutie
- Neinchiderea la intersectie
- Probleme de decizie – limbaje independente de context
- demonstratia faptului ca e nedecidabila problema echivalentei sau
- o demonstratie pentru o problema decidabila si o demonstratie pentru una nedecidabila din urmatoarea lista: apartenenta, finititudinea, trivialitatea, problema ambiguitatii
- Forma normala Chomsky
- definitie
- cei patru pasi pentru a construi forma normala Chomsky
- doi pasi din cei patru de aratat ca intr-adevar fac ceea ce se spune despre ei
|
|
|
|
|
|
|
|
|
2005-2006 - anul 1 - semestrul 2 - Domeniul de Informatica
|
|---|
|
|
|
|
|
|
- examen: 50% din care:
- teoretie 50%
- probleme 50%
- este nevoie de minim 5 la teorie ca sa iti faca media cu nota de la probleme altfel se pica
- laborator: 50%
- nu se face prezenta
|
|
- John E. Hopcroft, Jeffrey D. Ullman - "Introduction to Automata Theory, Languages and Computation" - Addison-Wesley 1979
|
|
- grupa 131:
- Proprietati de inchidere ale limbajelor INDEPENDENTE DE CONTEXT.
- Sa se determine un AUTOMAT FINIT DETERMINIST cu numar MINIM de stari care accepta limbajul
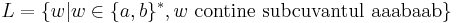
- La punctul 1 se cere exact teoria din curs
- La punctul 2 se primesc punctaje partiale daca automatul nu este minimal, sau daca nu este determinist
- grupa 132:
- Automate pushdown.
- Fiind dat un limbaj regulat L sa se dem ca
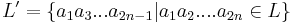 este si el regulat. este si el regulat.
- grupa 133
- sa se construiasca gramatica (automatul) care genereaza limbajul L = {an | n > = 1}.
![[ \{ b^mc | m \ge 1 \} \cup \{ d^p | p \ge 0 \} ]*](../images/math/5/b/7/5b7a56033b649f45e5c0272267665a72.png)
- sa se construiasca automatul push-down pornind de la limbajul
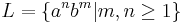 sau asemanator sau asemanator
- subiectul a fost dat pentru cei care nu au stiut subiectul de teorie si au cerut inchidere pentru limbaje regulate in loc CF, cu o reducere din punctajul total
- grupa 141
- Gramatici independente de context si automate stiva.
- teoria privind g.i.c. si a.p.d. (definitii, derivari in gramatica, tranzitii extinse in automat, limbajul gramaticii, cele doua tipuri de limbaje pentru automate, enunturile celor doua propozitii de echivalenta a celor doua tipuri de limbaje si enunturile celor doua teoreme de echivalenta g.i.c. respectiv a.p.d.)
- doua demonstratii, la alegere, (o propozitie si o teorema)
- Construiti un AF care sa recunoasca limbajul L si pe urma aplicati algoritmul de minimizare unde,
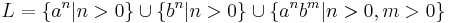 . .
- pentru constructia af fara minimizare se primeste peste jumatate din punctaj
- nota finala =
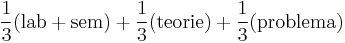
- grupa 142
- Probleme de decizie pe clasa limbajelor independente de context. (10 pct)
- Sa se construiasca un automat care accepta limbajul:
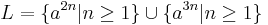 ( 10 pct) ( 10 pct)
- pentru construirea unui automat nederminist, se acorda 5 pct;
- pentru construirea unui automat determinist, se acorda 8 pct;
- pentru minimizarea automatului determinist obtinut, se acroda 10 pct;
- nota finala =
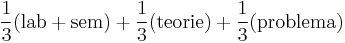
- grupa 153
- Proprietati de inchidere a limbajelor regulate (nr. 2 dictat la curs)
- Se da un limbaj regulat L si
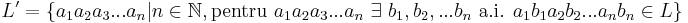 . Sa se demonstreze ca L' este regulat. . Sa se demonstreze ca L' este regulat.
|
|
|
|
|
|
|
|
|
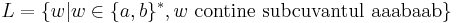
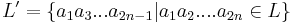 este si el regulat.
este si el regulat.
![[ \{ b^mc | m \ge 1 \} \cup \{ d^p | p \ge 0 \} ]*](../images/math/5/b/7/5b7a56033b649f45e5c0272267665a72.png)
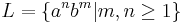 sau asemanator
sau asemanator
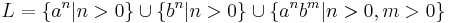 .
.
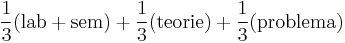
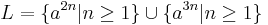 ( 10 pct)
( 10 pct)
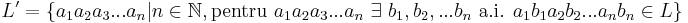 . Sa se demonstreze ca L' este regulat.
. Sa se demonstreze ca L' este regulat.
