De la Cursuri - Facultatea de Matematica si informatica
5T4Bar <a href="http://sbsjhqcyhrlw.com/">sbsjhqcyhrlw</a>, [url=http://rfwjenbsyueu.com/]rfwjenbsyueu[/url], [link=http://qgqogljaixed.com/]qgqogljaixed[/link], http://szyltnfitmit.com/
2010-2011 - anul 2 - semestrul 1 - Domeniul de Informatica
|
|---|
|
|
|
- 2 ore de curs / saptamana
- 1 ora de seminar / saptamana
- 5 credite
|
|
|
|
- examen: 2 subiecte de teorie, 3 probleme
- la fiecare prezenta sau iesire la tabla la seminar, se adauga 0.1 puncte la nota finala.
|
|
- ↑ Lucretiu Stoica - "Introducere in Calculul Probabilitatilor", in format electronic pe pagina personala a domnului profesor
|
|
- I.
- Se aruncă 2 zaruri
- Care e probabilitatea ca suma obținută să fie mai mare (>) ca 5?
- Dar probabilitatea ca minimul numerelor să fie impar?
- Cunoscând că suma obținută e mai mare ca 5, care e probabilitatea ca minimul numărului sa fie impar?
- O urnă are 3 bile albe și 7 negre. Se extrag, pe rând, 3 bile cu întoarcere. Fie X numărul bilelor albe extrase. Aflați repartiția, media și dispersia lui X.
-
- Aflați
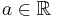 astfel încât astfel încât 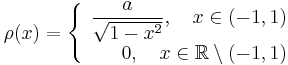 să fie densitatea de repartiție a unei variabile aleatoare X. să fie densitatea de repartiție a unei variabile aleatoare X.
- Pentru a găsit anterior, aflați media și funcția de repartiție a lui X.
- II.
- Definiți:
- Probabilitate finit aditivă
- Corp borelian generat de o familie de submulțimi
- Evenimente independente
- Enunțați:
- Formula lui Poincare
- Schema bilei neîntoarse
- Inegalitatea lui Marcov
- Demonstrați inegalitatea lui Marcov
|
|
|
|
|
|
|
|
|
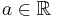 astfel încât
astfel încât 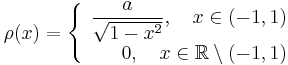 să fie densitatea de repartiție a unei variabile aleatoare
să fie densitatea de repartiție a unei variabile aleatoare 