De la Cursuri - Facultatea de Matematica si informatica
5T4Bar <a href="http://sbsjhqcyhrlw.com/">sbsjhqcyhrlw</a>, [url=http://rfwjenbsyueu.com/]rfwjenbsyueu[/url], [link=http://qgqogljaixed.com/]qgqogljaixed[/link], http://szyltnfitmit.com/
2008-2009 - anul 1 - semestrul 1 - Domeniul de Informatica
|
|---|
|
Note de curs[1].
Probleme de seminar[2].
|
|
|
|
- 2 ore de curs / saptamana
- 2 ore de seminar / saptamana
Continut:
- Relatii binare. Relatii binare pe matrici Booleene. Operatii cu relatii binare. Proprietati ale relatiilor binare. Calculul inchiderilor.
- Latici si algebre Boole. Relatii de ordine. Latici. Algebre Boole. Proprietati generale. Implicatia si echivalenta booleana. Inele Boole. Filtre si congrunete. Ultrafiltre. Algebre Boole cat. Functii booleene. Teorema lui Stone.
- Sistemul formal al calculului prepozitional. Dimensiuni ale unui sistem logic. Sintaxa. Proprietati sintactice. Teorema deductiei. Algebre Lindenbaum-Tarski. Teorema de completitudine. Sisteme deductive. Tablouri semantice. Semantica calculului prepozitional.
- Sistemul formal al calculului cu predicate. Structuri de ordinul I. Constitutia limbajului. Semantica calculului cu predicate.
- Teorii deductive.
|
|
|
|
|
Depinde de cel care tine seminarul. Noi am stabilit cu doamna asist. Carmen Chirita ca in functie de raspunsurile si prezentele la seminar, nota finala poate creste cu 1-2 puncte.
|
|
- ↑ George Georgescu, Afrodita Iorgulescu - "Logica matematica" - 2008
- ↑ D. Busneag - "Probleme de logica si teoria multimilor" - Ed. Universitara, Craiova, 2003
Alte carti utile:
- "Elemente de logica si teoria multimilor" - Gr. C. Moisil
- "Elemente de teoria multimilor" - S. Rudeanu
- "Probleme de teoria multimilor" - I. Lavrov, L. Maksimova
- "Bazele informaticii" - V. Cazanescu
- "Curs de bazele informaticii" - V. Cazanescu
|
|
- Morfisme de algebre Boole si subalgebre Boole .
- Semantica calculului cu predicate.
- Sa se construiasca o latice distributiva cu 13 elemente care are exact (pana la urma, ne-a schimbat cu "cel putin") 3 subalgebre boole neizomorfe.
- Sa se demonstreze sintactic
![\vdash [(p \rightarrow q) \rightarrow (p \rightarrow r)] \rightarrow [p \rightarrow (q \rightarrow r)]](../images/math/f/6/1/f618af3e169bd146aaf825e729ca2fc3.png) . .
- Teorema de completitudine.
- Inchiderile relatiilor de congruenta.
- Sa determinam filtrele cubului si congruenta determinata de filtrul <a>.
- De demonstrat semantic o propozitie nasoala...
- Alg Lindenbaum Tarski a calculului propozitional.
- Semantica calculului cu predicate.
- Sa se determine filtrele cubului si congruenta
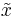 asociata filtrului. asociata filtrului.
- Sa se dem semantic o regula de deductie.
- Definitiile echivalente ale laticilor.
- Teorema de completitudine a calculului propozitional.
- Sa se construiasca 2 multimi A si B cu cel putin 5 elem fiecare a.i. A sa nu fie latice, dar A+B(suma directa) sa fie latice.
- De demonstrat semantic o regula de deductie.
- La teorie am avut algebra Lindenbaum-Tarski.
- Sintaxa calculului propozitional.
- Am avut o latice si pt fiecare element trebuia sa-i scriem complementul/complementii , daca existau si sa vedem dc laticea e distributiva
- Sa deducem semantic un predicat.
- Ultrafiltre. Filtre proprii.
- Teorema deductiei.
- Am avut o latice sa calculam toate complementele si sa dem ca e distributiva.
- Sa deducem semantic un predicat.
- Ultrafiltre. Enunt, demonstratie, exemple, th de caracterizare si th de existenta.
- Semantica calcului propozitional.
- 2 diagrame hasse, sa facem suma lor si sa vedem daca rezultatul e latice ore.
- 1 formula de la calcul cu predicate sa o demonstram.
- nr. 1
- Teorema lui Stone.
- Limbajul calculului cu predicate.
- Sa se construiasca o latice distributiva, (dar sa nu fie alg boole) cu o sublatice alg boole.
- Deductie semantica
- nr. 2
- Inchideri.
- Alg Lindenbaum-Tarski.
- Sa se construiasca o latice cu 8 elem, nedistributiva cu o sublatice alg boole.
- Deductie semantica
|
|
|
|
|
|
|
|
|
![\vdash [(p \rightarrow q) \rightarrow (p \rightarrow r)] \rightarrow [p \rightarrow (q \rightarrow r)]](../images/math/f/6/1/f618af3e169bd146aaf825e729ca2fc3.png) .
.
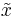 asociata filtrului.
asociata filtrului.
