- Grupa 231
- pentru b0,b1,b2,b3 scrieti schema de casteljau
- se dau 2 cubre bezier cu polig de control (b0,b1,b2)(b2,b3,b4). practic intrarea este b0,b1,...,b6. sa se scrie un alg prin care sa se determine daca cele 2 curbe au racord de clasa gc1 sau de clasa c1 in b2. (exact cum a facut in anexa C)
- se da M = {a0,a1,...,a5}. sa se determine P a.i. P U M sa aiba in partea superioara a infasorii convexe NUMAI 5 puncte (vezi multimea Ls din scanarea Graham)
- se dau 4 puncte prin coordonatele cardeziene (care formau un patrat). sa se deseneze diagrama voronoi
- se dau P0 si Pend. sa se scrie tabelul pentru algoritmul lui Bresenham
- Grupa 232
- (5p) Calculati curba rational patratica r(t) cunoscand b0,b1,b2.
- (15p) Scrieti un algoritm care stabileste daca un punct p(beta,6) apartine tangentei la curba bezier b data de b0,b1,b2,b3 in punctul b(1).
- (10p) Aplicati metoda din demonstratia teoremei galeriei de arta pentru o posibila amplasare a camerelor de supraveghere pentru un poligon determinat de P0...P9 dat.
- (10p) Fie M o multime cu 4 puncte date. Pozitionati un punct P a.i. diagrama Voronoi corespunzatoare multimii
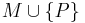 sa aiba exact 4 muchii de tip semidreapta ( si oricate muchii de alt tip ). sa aiba exact 4 muchii de tip semidreapta ( si oricate muchii de alt tip ).
- (10p) DDA pentru P0 = (41,31) si Pend = (51,38) ( vroia doar tabelul )
- Grupa 233
- (5p) Fie (b0,b1,b2,b3) polig de control al unei curbe Bezier. b0 = (4,5), b1 = (2,1), b2 = (8,1), b3 = (10,7). Scrieti schema de Casteljau pentru
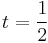 . .
- (15p)
![b:[0,1] \rightarrow \mathbb{R}^2 \mbox{. } b_0=(\alpha-3,2) \mbox{, } b_1=(3,2) \mbox{, } b2=(2+\beta,4-\beta)](../images/math/7/5/3/753cd4f6f5d4bb0650d4c47589339fc1.png) . Verificati daca tangentele la curba b in punctele b(0) si b(1) sunt perpendiculare sau coincid. . Verificati daca tangentele la curba b in punctele b(0) si b(1) sunt perpendiculare sau coincid.
- (10p) M = {P1,...P10,Q1,...Q10,R1,...R10}; Pi = (i − 1,i − 1), Qi = (0,i), Ri = (i,0)
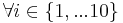 . Se cere lista finala Ls a varfurilor care determina marginea superioara a frontierei acoperirii convexe a lui M, parcursa in sensul acelor de ceasornic, furnizata de alogritmul lui Graham. Justificati. . Se cere lista finala Ls a varfurilor care determina marginea superioara a frontierei acoperirii convexe a lui M, parcursa in sensul acelor de ceasornic, furnizata de alogritmul lui Graham. Justificati.
- (10p) Dati exemple de multime de puncte din
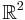 care sa admita o triangulare continand 7 muchii. Precizati numarul de triunghiuri ale acestei triangulari. care sa admita o triangulare continand 7 muchii. Precizati numarul de triunghiuri ale acestei triangulari.
- (10p) La reprezentarea unui segment folosind algoritmul lui Bresenham sunt selectati 16 pixeli (inclusiv extremitatile segmentului) si parametrul de decizie initial este p0 = 3. Calculati panta dreptei suport a segmentului, stiind ca e pozitiva si subunitara.
- Grupa 234
- (5pct) Se da
![b:[0,1] \rightarrow \mathbb{R}^2](../images/math/f/8/a/f8add10978d55a2c2514d11436dd56e3.png) si b0,b1,b2 si se cere forma Bernstein. si b0,b1,b2 si se cere forma Bernstein.
- (15pct) Se dau punctele b0,b1,b2,b3,b4. Stiind ca
![b:[1,2] \rightarrow \mathbb{R}^2](../images/math/f/8/f/f8fa9fc87566395c3e0dd2526a65f1ac.png) e curba Bezier asociata poligonul de control (b0,b1,b2) si e curba Bezier asociata poligonul de control (b0,b1,b2) si ![bb:[2,3] \rightarrow \mathbb{R}^2](../images/math/f/f/8/ff84e4200919636904f6708d241a2e1d.png) e curba Bezier asociata poligonul de control (b2,b3,b4) scrieti un algoritm care sa determine pozitia relativa a tangentelor la curba b si bb in punctul b2. e curba Bezier asociata poligonul de control (b2,b3,b4) scrieti un algoritm care sa determine pozitia relativa a tangentelor la curba b si bb in punctul b2.
- (10pct) Dati exemplu de o multime M in
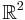 cu 8 puncte a.i. Ls si Li sa aiba cate 4 puncte. cu 8 puncte a.i. Ls si Li sa aiba cate 4 puncte.
- (10pct) Se dau 5 puncte in
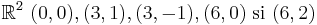 . Se cere sa se determine triangularea Delaunay a celor 5 puncte, folosind diagrama Voronoi. . Se cere sa se determine triangularea Delaunay a celor 5 puncte, folosind diagrama Voronoi.
- Grupa 241
- (5 pct) se dau b0,b1,b2,b3 si se cere curba b(t), cu polinoame Bernstein.
- (15 pct) se dau b0,b1,b2 si se cere un algoritm care se determine daca tangenta la curba in punctul t0 este paralela sau nu cu dreapta OX.
- (10 pct) Se dau {A1,A2,...,A11},Ai = (i,3 + ( − 1)i). Se cere lista finala a puctelor de pe frontiera, cu algoritmul Graham Scan. + Justificare (cateva cuvinte)
- (10 pct) Se dau P1,...,P5 se cere sa se dea un exemplu de coordonate pt P6 a.i. triangularea sa aibe exact 10 muchii. + Justificare (cateva cuvinte)
- (10 pct) Se dau P0 si Pend si se cere sa se scrie ce patratele urmau sa fie selectate prin algoritmul DDA.
- Grupa 244
- Scrieti explicit curba Bezier rational patratica pentru b0 = ( − 1,1), b1 = (0,0), b2 = (1,1), λ1 = 1, λ2 = 1, λ3 = 3.
- Se da poligonul de control pt curba Bezier: b0 = (α − 3,2), b1 = (3,6), b2 = (7,2). Scrieti un algoritm care sa stabileasca daca punctul P = (β − 4,2β − 4) apartine tangentei la curba in punctul
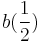 . .
- Fie multimea de puncte
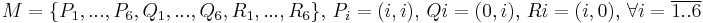 . Precizati numarul de triunghiuri si numarul de muchii ale unei triangulari. . Precizati numarul de triunghiuri si numarul de muchii ale unei triangulari.
- Dati exemplu de puncte din
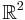 astfel incat diagrama Voronoi are exact 3 muchii de tip segment. Explicati constructia facuta. Spuneti numarul varfurilor diagramei Voronoi. astfel incat diagrama Voronoi are exact 3 muchii de tip segment. Explicati constructia facuta. Spuneti numarul varfurilor diagramei Voronoi.
- Algoritmul Bresenham pentru P0 = (37,41), Pend = (47,48).
|
|
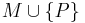 sa aiba exact 4 muchii de tip semidreapta ( si oricate muchii de alt tip ).
sa aiba exact 4 muchii de tip semidreapta ( si oricate muchii de alt tip ).
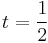 .
.
![b:[0,1] \rightarrow \mathbb{R}^2 \mbox{. } b_0=(\alpha-3,2) \mbox{, } b_1=(3,2) \mbox{, } b2=(2+\beta,4-\beta)](../images/math/7/5/3/753cd4f6f5d4bb0650d4c47589339fc1.png) . Verificati daca tangentele la curba b in punctele b(0) si b(1) sunt perpendiculare sau coincid.
. Verificati daca tangentele la curba b in punctele b(0) si b(1) sunt perpendiculare sau coincid.
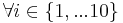 . Se cere lista finala Ls a varfurilor care determina marginea superioara a frontierei acoperirii convexe a lui M, parcursa in sensul acelor de ceasornic, furnizata de alogritmul lui Graham. Justificati.
. Se cere lista finala Ls a varfurilor care determina marginea superioara a frontierei acoperirii convexe a lui M, parcursa in sensul acelor de ceasornic, furnizata de alogritmul lui Graham. Justificati.
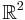 care sa admita o triangulare continand 7 muchii. Precizati numarul de triunghiuri ale acestei triangulari.
care sa admita o triangulare continand 7 muchii. Precizati numarul de triunghiuri ale acestei triangulari.
![b:[0,1] \rightarrow \mathbb{R}^2](../images/math/f/8/a/f8add10978d55a2c2514d11436dd56e3.png) si
si ![b:[1,2] \rightarrow \mathbb{R}^2](../images/math/f/8/f/f8fa9fc87566395c3e0dd2526a65f1ac.png) e curba Bezier asociata poligonul de control
e curba Bezier asociata poligonul de control ![bb:[2,3] \rightarrow \mathbb{R}^2](../images/math/f/f/8/ff84e4200919636904f6708d241a2e1d.png) e curba Bezier asociata poligonul de control
e curba Bezier asociata poligonul de control 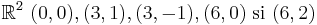 . Se cere sa se determine triangularea Delaunay a celor 5 puncte, folosind diagrama Voronoi.
. Se cere sa se determine triangularea Delaunay a celor 5 puncte, folosind diagrama Voronoi.
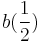 .
.
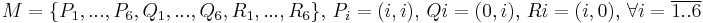 . Precizati numarul de triunghiuri si numarul de muchii ale unei triangulari.
. Precizati numarul de triunghiuri si numarul de muchii ale unei triangulari.
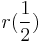 .
.
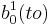 , respectiv
, respectiv 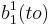 .
.
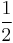 .
.
